Attention Mechanism in Image Captioning

这里会从Attention Mechanism的角度介绍3篇关于Image Captioning的文章。

Image Captioning with Semantic Attention

[1] Quanzeng You, Hailin Jin, Zhaowen Wang, Chen Fang & Jiebo Luo(2016): Image Captioning with Semantic Attention. CoRR, abs/1603.03925, https://arxiv.org/abs/1603.03925

这篇文章是[2]的引用，并作为性能的比较。这篇文章是从Attention的角度来提升Image Caption性能的。文章指出，“现存”的方法只有两种形态：抓住图片的整体内容然后转化为句子的top-down方法，或者从图片的不同方面进行描述然后组合在一起的bottom-up方法。并没有能够将两者组合在一起的方法。Top-down是“目前”的state-of-the-art的方法，但是它有自己的问题：很难参与到细节调整当中去——一些细节可能对于描述图片是十分重要的。Bottom-up当然不存在这个问题了，因为它们对不同尺度的图片操作是比较自由的，但是Bottom-up没有一个end-to-end的formulation（规则）。

这篇文章通过semantic attention model推出了一个end-to-end的结合top-down和bottom-up的Image Captioning方法。

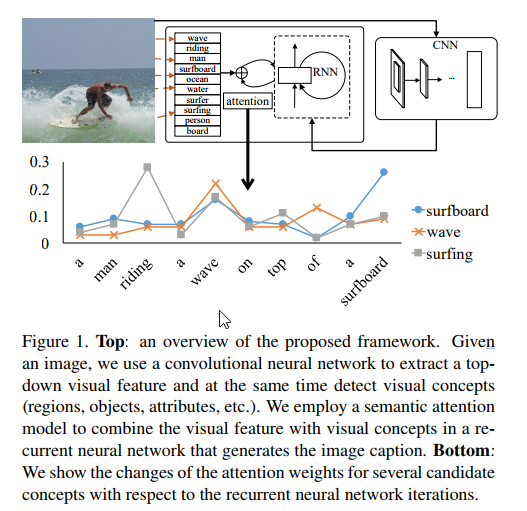
“Our definition for semantic attention in image captioning is the ability to provide a detailed, coherent description of semantically important objects that are needed exactly when they are needed.” 在image captioning中，语义注意力定义为：能够在目标被需要时提供详细的、连贯的描述的能力。有以下性质：

• 能够注意图片中语义上重要的概念和区域；
• 在有多个概念的时候能够有合适的权重去处理；
• 能够根据任务的状态自动调整。

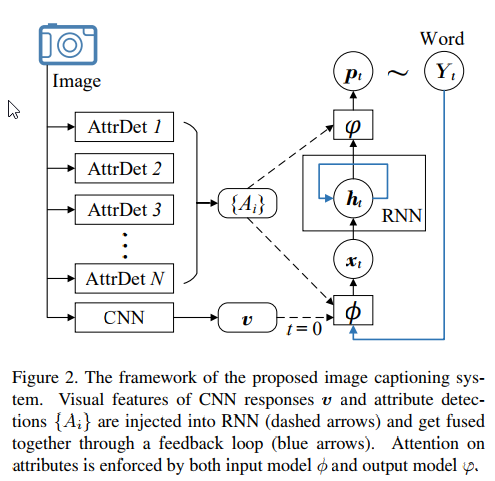
其中 \[x_0=\phi_0(v)=W^{x,v}v\] \[h_t=RNN(h_{t-1},x_t)\] \[Y_t\sim p_t=\varphi(h_t,{A_i})\] \[x_t=\phi(Y_{t-1},{A_i}),t>0\]

关于如何得到${A_i}$的

一种方法是：搜索，在数据集中搜索GoogLeNet的feature相近的图片的标注中出现频率较高的单词。另一种方法是multi-label的分类器、FCN。两种方法是一起使用的。

Input Attention model $\phi$

每一个$A_i$前有一个系数$\alpha_t^i$，表示$A_i$在$t$时刻的输入注意力权重。这个系数与$A_i$以及前一时刻的输出$Y_{t-1}$有关。由于$A_i$以及$Y_{t-1}$都表示一个单词，可以用长度为$|\mathcal{Y}|$的one-hot向量表示，分别为$y_{t-1}$和$y^i$。那么 \[\alpha_t^i= softmax(y_{t-1}^T \widetilde{U}y^i)\] 由于$|\mathcal{Y}|$比较大，导致参数很多，因此在这里对$y_{t-1}$和$y^i$由高维映射到低维，方法有Word2Vec或者Glove（实验用法）。令word embedding矩阵为$E\in\mathbb{R}^{d\times|\mathcal{Y}|}$，其中$d$远小于单词表的大小。则： \[\alpha_t^i= softmax(y_{t-1}^T E^T UE y^i)\] 这样就大大减少了参数的数量。$x_t$的计算方法如下 \[x_t=\phi(Y_{t-1},{A_i})=W^{x,Y}(Ey_{t-1}+diag(w^{x,A})\sum\limits_{i}\alpha_t^iEy^i)\] 其中$W^{x,Y}$是为了将输入由$d$维映射到$m$维（即所需的输入的维度）。而$diag(w^{x,A})$是由向量$w^{x,A}\in\mathbb{R}^d$形成的对角矩阵，向量中的每个元素表示不同维度的重要程度。

Output Attention model $\varphi$

与$\phi$相似。$\beta_t^i$表示在$t$时刻$A_i$在输出端的留心程度，它与前一时刻的输出的嵌入$y^i$和当前LSTM的状态$h_t$有关。计算方式如下: \[\beta_t^i=softmax(h_t^T V\sigma(Ey^i) )\] 其中$V$是$n\times d$的矩阵。这样$p_t$的计算公式如下 \[p_t=softmax(E^T W^{Y,h}(h_t+diag(w^{Y,A})\sum\limits_{i}\beta_t^i\sigma(Ey^i) ))\]

Image Captioning with Object Detection and Localization

[2] Zhongliang Yang, Yu-Jin Zhang, Sadaqat ur Rehman & Yongfeng Huang(2017): Image Captioning with Object Detection and Localization. CoRR, abs/1706.02430, https://arxiv.org/abs/1706.02430

这篇文章可参见之前的post。

这篇文章的detection部分使用的Faster R-CNN。对于每一张图片得到得分前n名的目标，每个目标用用一个d维的向量来表示$obj_i$（Fast R-CNN的fc7），并且对于每一个目标在图片上将目标以外的所有区域像素置为全图的均值。然后将处理后的图片作为VGG的输入将得到的该目标的位置向量$loc_i\in\mathbb{R}^t$。那么$A_i=[obj_i;loc_i]\in\mathbb{R}^{d+t}$。

生成单词也是通过LSTM，与NIC不同的是，LSTM中在$j$时刻接收$w_{j-1}$的同时也会接收$z_j$，即映射到同一维之后做线性叠加。而$z_j$是$A_i$在$j$时刻的某种线性组合$z_j=\sum_{i=1}^{n}\alpha_{ji}A_i$，其中$\alpha_{ji}$是权值，且 \[\alpha_{ji}=softmax(e_{ji})=softmax(f_{att}(A_i,h_{j-1}))\] 这里$f_{att}$是$h_{j-1}$条件下的多层感知机，输入是$A_i$，输出是一个实数scalar。

Bottom-Up and Top-Down Attention for Image Captioning and VQA

[3] Peter Anderson, Xiaodong He et.al.(2017): Bottom-Up and Top-Down Attention for Image Captioning and VQA. CoRR, abs/1707.07998, https://arxiv.org/abs/1707.07998

对于已经通过nms算法（非极大值抑制算法）选定的$k$个区域$v_i\in\mathbb{R}^{2048}$表示这个区域均化卷积feature。

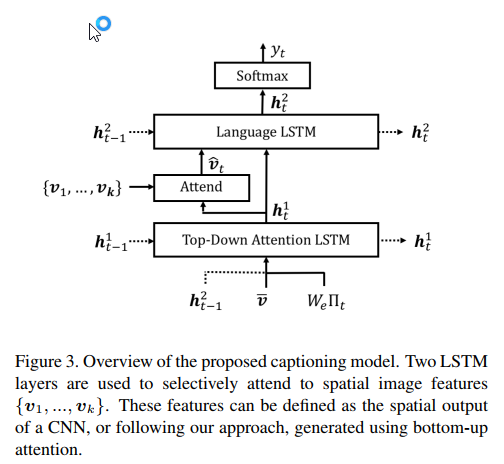
整个decoder部分包含两个LSTM，分别称之为LSTM1和LSTM2。在$t$时刻，LSTM1的输入$x_t^1$由3部分拼接得到 \[x_t^1=[h_{t-1}^2,\bar{v},W_e\Pi_t]\] 其中$\bar{v}=\frac{1}{k}\sum_{i}v_i$，$\Pi_t$为$t$时刻输入的单词，$W_e$为单词嵌入矩阵，大小为$E\times\Sigma$。得到的$x_t^1$为$M+V+E$维的。这时LSTM1的状态由原来的$h_{t-1}^1$变为$h_{t}^1$。LSTM之后增加了一个注意力机制，每个目标feature的权重计算方式如下： \[a_{i,t}=w_a^T\tanh(W_{va}v_i+W_{ha}h_t^1)\] \[\alpha_t=softmax(a_t)\] 其中$w_a$是$H$维的参数，后面括号里的两个$W$是要把相乘的向量映射到$H$维。这样 \[\hat{v_t}=\sum\limits_{i=1}^k \alpha_{i,t}v_i \] 这样就得到了LSTM2的输入$x_t^2=[\hat{v_t},h_t^1]$。LSTM2的输出$h_t^2$经全连接层之后便得到了词分布向量 \[p(y_t|y_{1:t-1})=softmax(W_ph_t^2+b_p)\]

About Codes

• 代码方面，我找到了上面这篇文章的源代码，不过是caffe的。
• tf-faster-rcnn，目前可以跑test，没有尝试train
• 代码方面需要提升，通过captioning来提高。